 (Fig. 1)
(Fig. 1)
We have already seen how to train linear networks by gradient descent. In trying to do the same for multi-layer networks we encounter a difficulty: we don't have any target values for the hidden units. This seems to be an insurmountable problem - how could we tell the hidden units just what to do? This unsolved question was in fact the reason why neural networks fell out of favor after an initial period of high popularity in the 1950s. It took 30 years before the error backpropagation (or in short: backprop) algorithm popularized a way to train hidden units, leading to a new wave of neural network research and applications.
 (Fig. 1)
(Fig. 1)
In principle, backprop provides a way to train networks with any number of hidden units arranged in any number of layers. (There are clear practical limits, which we will discuss later.) In fact, the network does not have to be organized in layers - any pattern of connectivity that permits a partial ordering of the nodes from input to output is allowed. In other words, there must be a way to order the units such that all connections go from "earlier" (closer to the input) to "later" ones (closer to the output). This is equivalent to stating that their connection pattern must not contain any cycles. Networks that respect this constraint are called feedforward networks; their connection pattern forms a directed acyclic graph or dag.
|
| |
|
| |
|
| |
|
|
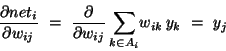
To compute this gradient, we thus need to know the activity and the error for all relevant nodes in the network.
Note that before the activity of unit i can be calculated, the activity of all its anterior nodes (forming the set Ai) must be known. Since feedforward networks do not contain cycles, there is an ordering of nodes from input to output that respects this condition.

Of the three factors inside the sum, the first is just the error of node i. The second is

while the third is the derivative of node j's activation function:
For hidden units h that use the tanh activation function, we can make use
of the special identity
tanh(u)' = 1 - tanh(u)2, giving us
Putting all the pieces together we get
Note that in order to calculate the error for unit j, we must first know the error of all its posterior nodes (forming the set Pj). Again, as long as there are no cycles in the network, there is an ordering of nodes from the output back to the input that respects this condition. For example, we can simply use the reverse of the order in which activity was propagated forward.