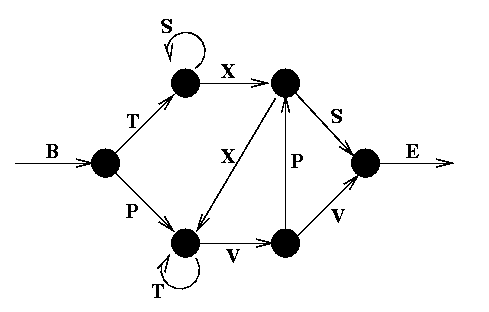
 (Fig.
1)
(Fig.
1)Consider the following string generator, known as a Reber grammar:
 (Fig.
1)
(Fig.
1)We start at B, and move from one node to the next, adding the symbols we pass to our string as we go. When we reach the final E, we stop. If there are two paths we can take, e.g. after T we can go to either S or X, we randomly choose one (with equal probability). In this manner we can generate an infinite number of strings which belong to the rather peculiar Reber language. Verify for yourself that the strings on the left below are possible Reber strings, while those on the right are not.
| "Reber" | "Non-Reber" |
|---|---|
| BTSSXXTVVE | BTSSPXSE |
| BPVVE | BPTVVB |
| BTXXVPSE | BTXXVVSE |
| BPVPXVPXVPXVVE | BPVSPSE |
| BTSXXVPSE | BTSSSE |
What are the set of symbols which can "legally" follow a T?. An S can follow a T, but only if the immediately preceding symbol was a B. A V or a T can follow a T, but only if the symbol immediately preceding it was either a T or a P. In order to know what symbol sequences are legal, therefore, any system which recognizes reber strings must have some form of memory, which can use not only the current input, but also fairly recent history in making a decision.
While the Reber grammar represents a simple finite state grammar and has served as a benchmark for equally simple learning systems (it can be learnt by an Elman network), a more demanding task is to learn the Embedded Reber Grammar, shown below:
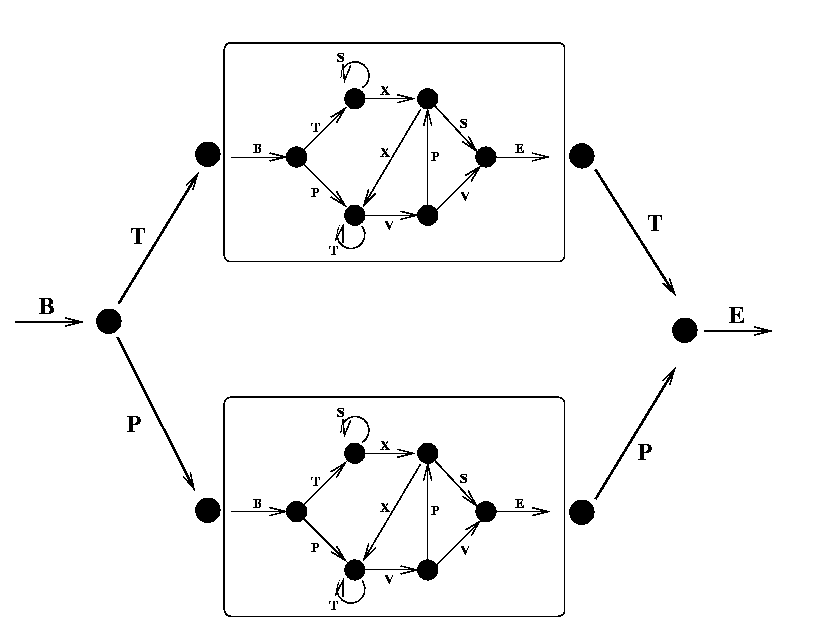 (Fig. 2)
(Fig. 2)Using this grammar two types of strings are generated: one kind which is made using the top path through the graph: BT<reber string>TE and one kind made using the lower path: BP<reber string>PE. To recognize these as legal strings, and learn to tell them from illegal strings such as BP<reber string>TE, a system must be able to remember the second symbol of the series, irrespective of the length of the intervening input (which can be as much as 50 or more symbols), and to compare it with the second last symbol seen. An Elman network can no longer solve this task, but RTRL can usually solve it (with some difficulty). More recent recurrent models can always solve it.